A General Approach for Exploiting Statistical Arbitrage Alphas 

Last week, I wrote a short article about statistical arbitrage trading in the real world.

Statistical arbitrage is a well-understood concept: find pairs or baskets of assets you expect to move together, wait for them to diverge, and bet on them converging again.

Simple enough.

But making it work, especially at scale, is a little more complicated.

A somewhat old-school approach takes pairs of correlated assets and trades them long-short together. This is the classic pairs trade.

But we don’t have to constrain ourselves to this approach.

And when we consider a more general approach, we find exploitable opportunities that may not work under the classic pairs trading paradigm.

For instance, trading a long-short portfolio of equity pairs is expensive and margin-intensive. The more general statistical arbitrage approach I’ll discuss here will greatly reduce costs and margin requirements.

In this article, I’ll share a general approach for managing a portfolio of statistical arbitrage trades. It involves navigating the trade-offs around maximising expected returns while minimising portfolio variance and trading costs.

Generalizing Statistical Arbitrage

When I use the term “statistical arbitrage”, I’m referring to any quantifiable, systematic, long-short, active trading.

A classic example is the basket reversion trade.

Imagine you have a bunch of assets and some criteria that allow you to predict whether those assets are expensive or cheap.

In practical terms, “expensive” means you expect it to go down, and “cheap” means you expect it to go up.

Then, you can rank all of your assets according to your criteria and aim to be:

• Very short the stuff that’s very expensive
• Slightly short the stuff that’s a bit expensive
• Slightly long the stuff that’s a bit cheap
• Very long with stuff that’s very cheap

The trade also seeks to minimize portfolio return variance by being about as short as it is long a bunch of similar assets. In other words, you aim to isolate the alpha embedded in the divergence of these similar assets and cancel out everything else.

So, you can consider it a reversion trade of effectively everything in the basket converging with fair value.

Of course, the implementation details can get a little complicated, but conceptually, it’s a very simple trade.

Conceptual Implementation of Statistical Arbitrage

Here’s a general setup for implementing a statistical arbitrage portfolio:

Let’s go through all the parts.

1. Estimate Expected Returns

The first step is to calculate expected returns. This is the most difficult and important part.

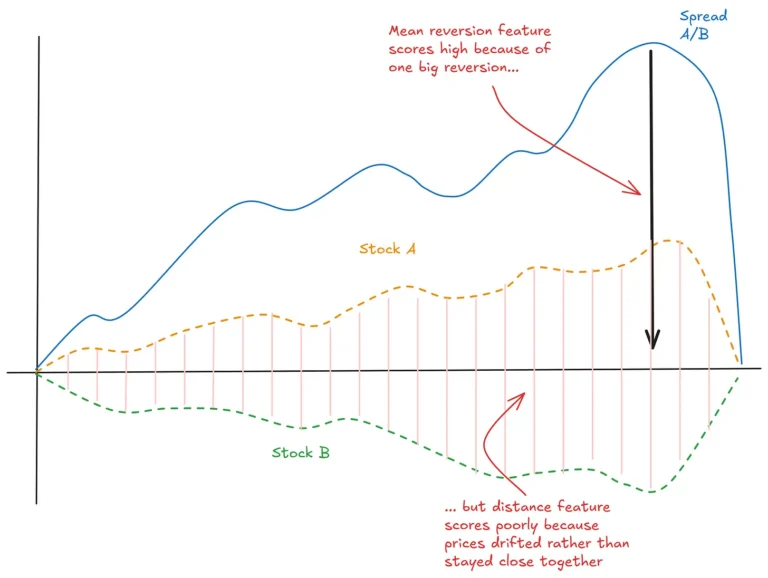
Your expected returns model will generally be the output of an extensive research process where you identify various features that predict future returns. Examples might include cross-sectional momentum or mean-reversion, microstructure effects, lead-lag relationships, carry, etc.

One useful metric for quantifying the effectiveness of a feature is the information coefficient, which measures the correlation between the feature and step-ahead returns.

We also like to consider how quickly the feature’s predictiveness decays over time. Alphas with high information coefficients are great, but in practice, we prefer alphas that decay slowly, as they are more forgiving to trade (rely less on execution skill), turnover less frequently, and can be harnessed with less trading (all things being equal).

Consider two momentum features as an example.

• The two features both have a correlation coefficient with hour-ahead returns of 0.05.
• The first feature has a shorter lookback period and decays quickly.
• The second feature has a longer lookback period and decays more slowly.

The second feature is more valuable because it requires less trading to harness.

We also prefer alphas that are uncorrelated with other alphas – these tend to give you more bang for your buck at the portfolio level.

Say you have several predictive features with different information coefficients and decay characteristics. You then need to combine them into an expected return for each asset. This usually involves up-weighting or down-weighting the different alphas depending on their characteristics, and perhaps scaling them to an understood range, such as using a z-score.

Useful tools for understanding your alphas and informing good decisions about how you combine them include:

• Scatterplots
• Ranks and sorts
• Information coefficient
• Information coefficient decay
• Autocorrelation function

This is a fairly big topic in itself. I’ll revisit it with some specific examples in a future article.

2. Minimising Variance

In traditional pairs trading, we would trade equally weighted long and short positions in correlated assets. However, in a more general statistical arbitrage approach, we can take advantage of asset relationships to reduce portfolio risk.

For example, instead of maximizing expected returns, we can consider the co-movement of different assets and adjust our positions accordingly. This means we may end up shorting assets that we expect to go up, but not as much as other assets, to reduce volatility.

If you were maximising expected returns, you’d simply get long the stuff you expect to go up the most.

But if we’re maximising risk-adjusted returns, shorting assets correlated with the highest expected return assets makes sense, even if we expect those to go up as well. Doing so essentially isolates the divergence and nets off the other risks – at least to the extent that our assets are exposed to the same risks.

As an aside, why would it be smart to reduce volatility? Because this tends to increase your long-run geometric expected returns, which lets you compound your money more effectively.

Including a risk model for the purposes of reducing portfolio variance usually implies doing some sort of constrained mean-variance optimisation (constrained because we usually want to consider real-world constraints such as leverage limits, beta-neutrality, or whatever else we are beholden to).

But the risk model doesn’t need to be based on an explicit optimisation – you can, for example, use simple heuristics such as equal dollar weight long-short, or slightly more complicated heuristics that reduce target exposures in assets that are on average more correlated to other things in the portfolio.

This is another fairly big topic and I’ll show you some examples in a future post.

3. Minimising Trading Costs

Reducing turnover is also crucial in making a statistical arbitrage portfolio work in the real world.

Every time you trade, you incur a cost – fees, spreads, market impact. And our costs are largely known (especially if we’re trading small and can ignore market impact). In contrast, our returns are uncertain (that’s why we refer to them as expected).

This implies that we don’t want to be naively whacking an edge – we need to do so in a cost-aware manner.

Here’s a really simple example to make it clear:

Consider three assets that have the following expected returns over the next day:

• Asset A: +0.5%
• Asset B: 0%
• Asset C: -0.1%

What’s the trade?

Well, assuming no interesting correlation relationships, you’d long asset A and short asset C.

You expect asset A to go up the most, and you expect asset C to go down the most. So that’s an easy trade.

But when you’ve actually got a position on, it’s not quite so clear-cut anymore.

We’re in a position where we’re long asset A and short asset C. Now the next day, we run our features again and obtain our expected return predictions:

• Asset A: +0.5%
• Asset B: -0.12%
• Asset C: -0.1%

Now we’re expecting the same return for asset A – a 0.5% increase. Asset C is also the same – a 0.1% decrease.

But our prediction for asset B is now -0.12%. It has the most negative expected return.

So if we had no positions on, we wouldn’t enter the positions we actually have. We would buy asset A, but we’d sell asset B.

But we are currently long asset A and short asset C.

If trading were free, we would get out of asset C and sell asset B instead. But trading isn’t free.

By switching positions, we would get an increase in expected returns of 0.02%. But returns are uncertain and there’s usually a huge amount of variance associated with our prediction.

On the other hand, know for a fact that trading out of C and into B is going to cost us money.

Now the question is, is the expected return that we get from shifting position significantly bigger than the known costs that we pay from shifting position? And in this case, we probably wouldn’t do the trade because our trading costs are very likely to be bigger than the expected return increase that we get from switching positions.

In reality, we need the expected return increase to be significantly bigger than our trading costs because we’ve got errors in our estimates. Our estimates are a distribution. You always want to give yourself some wiggle room.

You can make a similar example for a trade that would reduce portfolio variance. Depending on the costs of trading and the expected reduction in variance, you may be better off sticking with an existing position, especially if the existing exposure is correlated with the ideal exposure.

The main takeaway is that the positions that we have are a significant consideration (in addition to return and risk predictions) in what trading we should do to rebalance into new positions.

Like the variance reduction step, you can incorporate trading costs using simple heuristic rules or explicit optimisation. Again, I will show you some examples of this in a future article.

Managing Trade-offs

The approach I’ve outlined here is essentially an exercise in maximising return on investment by smart management of the trade-offs between expected returns, risk and trading costs.

Finding some predictive features is the most important part of the process because without a good return prediction, you simply don’t have a trade. Minimising variance and reducing turnover is not alpha.

But having a good return prediction is usually not enough – you need to be clever in how you harness it such that you maximise your long-term returns in the face of trading costs and whatever other constraints you’re under.

Statistical Arbitrage in Practice

In this article, I outlined a general approach to statistical arbitrage trading. But I left out many of the practical details, including:

• Ideas for predictive features
• Examples of exploring these features and quantifying their information coefficients and decay characteristics
• Combining alphas with different ICs and decay characteristics
• Using heuristics to navigate the return-risk-cost trade-off
• Using constrained optimisation to navigate the return-risk-cost trade-off

In future articles, I’ll provide examples of all of the above. If there are other topics you’d like to see, please let me know in the comments.