Working with Tidy Financial Data in tidyr
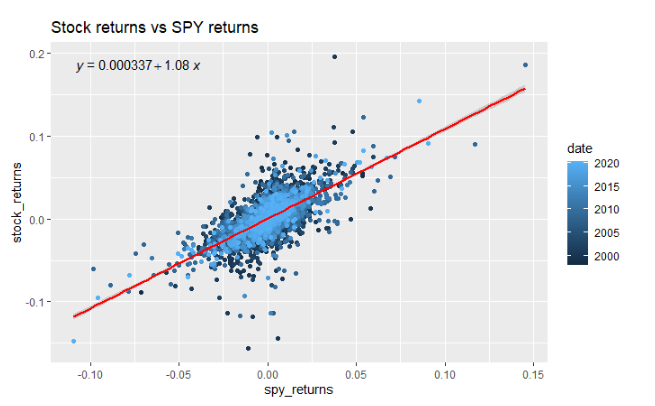
Holding data in a tidy format works wonders for one’s productivity. Here we will explore the tidyr package, which is all about creating tidy data. In particular, let’s develop an understanding of the tidyr::pivot_longer and tidyr::pivot_wider functions for switching between different formats of tidy data. In this video, you’ll learn: What tidy data looks like …